LES PRIORITÉS DES OPÉRATIONS DANS UNE ÉCUATION

ORDRE DES OPÉRATIONS :

1 - COMMENCEMENT DES OPÉRATIONS DE GAUCHE À DROITE

2 - SORTIR DES PARENTHÈSES

3 - FAIRE LES MULTIPLICATIONS ET DIVISIONS AVANT LES SOMMES ET LES SOUSTRACTION, DANS LA MESURE DU POSSIBLES

 

UNE ÉQUATION D'ALGÈBRE AVEC UNE incognita

((X+2) x 3 -4) ➗2 = 10 

((X +2) x 3 -4) = 10 x 2

((X +2) x 3 -4) = 20

3X + 6 – 4 = 20

3X + 2 = 20

3X = 20 – 2

3X = 18

X = 18➗3

X = 6

 

VÉRIFICATION DE LA VALEUR DE X

((6+2) x3-4) ➗2 = 10

((8) x 3-4) ➗2 = 10

(24 - 4)  ➗2 = 10

20 ➗2 = 10

10 = 10 

UNE AUTRE Version MÉCONNUE   

EXTRAIT DE L'ARTICLE

Une fois que l’on a compris cela, on peut trouver des équations avec de multiples solutions en ajoutant des carrés. Regardons par exemple l’équation suivante :

$(x^2-10{)}^2=36$.

On peut la représenter comme ceci :

Puis, le schéma suivant permet de trouver ses solutions :

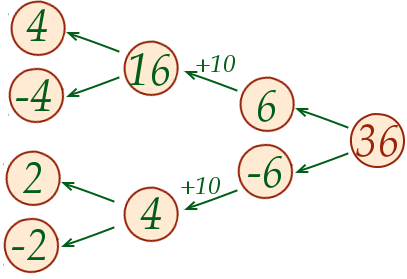
REMPLACEMENT DE X

(X² – 10)² = 36

(4² – 10)² = 36

(16 – 10)² = 36

(6)² = 36 

36 = 36

 

LA MÊME ÉQUATION SOUS UN AUTRE ANGLE

(X² – 10)² = 36

(X²)² + 100 = 36

(X²)² = 36 – 100

(X²)² = -64

 X² =

 

 

X² = -8

REMPLACER LA VALEUR DE X DANS L'ÉQUATION

(X² – 10)² = 36

(-8)² – 10² = 36

-64 + 100 = 36

36 = 36